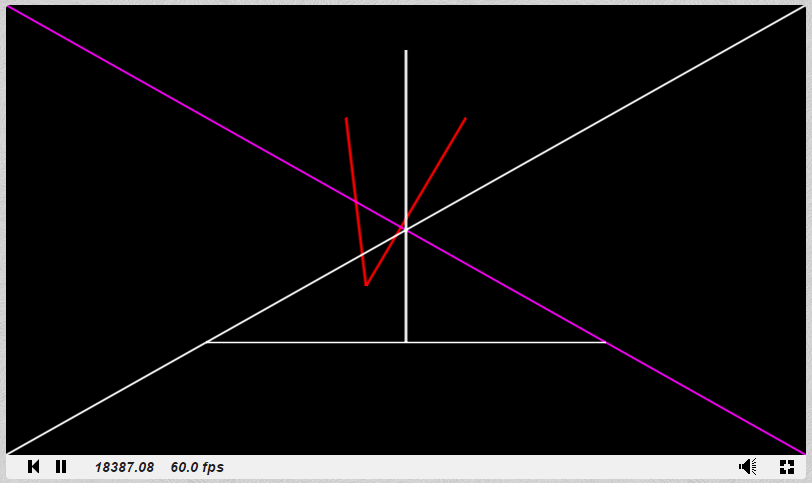
フラグメント・シェーダー(Shadertoy)で線分を書いてみようと思った。
Shadertoyのフラグメント・シェーダーは描画するピクセルごとにmainImage(out vec4 fragColor, in vec2 fragCoord)が呼ばれる。画面のピクセル個数分このmainImage()が呼ばれるのである。
この関数で描画色を決め、fragColorに色をセットする。fragCoordは描画するピクセルの座標位置が入る。
線分の描画の考え方としては「ピクセルが線分の描画範囲に入っている場合は指定の色で色付ける。」となる。つまり画面全部の点についてこの処理を行えば線分が描画できることになる。
で、その点が線分に含まれるかどうかのアルゴリズムはいろいろありそうだが、私は以下のように考えた。
- 現在のピクセルの座標を、描画したい線分の座標をとする。
- を通り、を通る直線に垂直に交わる直線と、を通る直線との交点をとする。
- ととの距離をとすると、が線の太さ以下であればその点を描画する。
上の考え方に沿って実装方法を考えた。
- を通る直線の方程式は
- を通り、と直交する直線の方程式は
- の交点を求める。式を式に代入する。
- 式を整理する。
- かつ であれば描画しない。
- を式(1)に代入しを求める。
- を求め、とする。であれば描画する。
もしくはの場合は特殊なケースとして場合分けをした。このあたりまで考えて実装した結果が以下である。
vec4 backcolor = vec4(0.,0.,0.,0.0);
vec4 line2(vec2 p3,vec2 p1,vec2 p2,float t,vec4 c){
float y2y1 = p2.y - p1.y;
float x2x1 = p2.x - p1.x;
float y3y1 = p3.y - p1.y;
float min_x = min(p1.x,p2.x);
float min_y = min(p1.y,p2.y);
float max_x = max(p1.x,p2.x);
float max_y = max(p1.y,p2.y);
if(y2y1 == 0.){
if(p3.x >= min_x && p3.x <= max_x){
return smoothstep(t/iResolution.y, 0., abs(y3y1) ) * c;
} else {
return backcolor;
}
}
if(x2x1 == 0.){
if((p3.y >= min_y) && (p3.y <= max_y)){
return smoothstep(t/iResolution.x, 0., abs(p1.x - p3.x) ) * c;
} else {
return backcolor;
}
}
float x4 = (x2x1 * x2x1 * p3.x + y3y1 * x2x1 * y2y1 + y2y1 * y2y1 * p1.x) / (y2y1 * y2y1 + x2x1 * x2x1);
if(x4 >= min_x && x4 <= max_x){
float y4 = y2y1 / x2x1 * (x4 - p1.x) + p1.y;
float d = length(p3 - vec2(x4,y4));
return smoothstep(t/iResolution.y, 0., d ) * c;
}
return backcolor;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 r = 2.0*vec2(fragCoord.xy - 0.5*iResolution.xy)/iResolution.xy;
fragColor = line2(r,vec2(-1.0,-1.0),vec2(1.0,1.0),3.,vec4(1.0,1.0,1.0,1.0));
fragColor += line2(r,vec2(0.0,-0.5),vec2(0.0,0.8),3.,vec4(1.0,1.0,1.0,1.0));
fragColor += line2(r,vec2(-0.5,-0.5),vec2(0.5,-0.5),3.,vec4(1.0,1.0,1.0,1.0));
fragColor += line2(r,vec2(1.0,-1.0),vec2(-1.0,1.0),3.,vec4(1.0,0.0,1.0,1.0));
fragColor += line2(r,vec2(-0.1,-0.25),vec2(-0.15,0.5),3.,vec4(1.,0.,0.,1.));
fragColor += line2(r,vec2(-0.1,-0.25),vec2(0.15,0.5),3.,vec4(1.,0.,0.,1.));
}
https://www.shadertoy.com/view/4ltSzH
実際Shadertoyのコードを読むと、もっと簡単に書いている方もいる。ベクトルの考え方を導入することによってね。
https://www.shadertoy.com/view/Xd2XWR
上の線分のコードを改造すると以下となる。
// Thanks Iñigo Quilez!
vec4 float line3( in vec2 p, in vec2 a, in vec2 b,in float t,in vec4 c )
{
vec2 pa = p - a;
vec2 ba = b - a;
float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
float d = length( pa - ba*h );
return smoothstep(t/iResolution.y, 0., d ) * c;
}
うーむ。このコードはすごいな。。